Loading...
Searching...
No Matches
CompositeRegion< N > Class Template Referenceabstract
union of arbitrary number of regions More...
#include <region_2.h>
Inheritance diagram for CompositeRegion< N >:
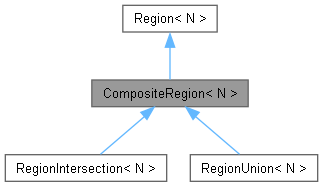
Collaboration diagram for CompositeRegion< N >:
Public Member Functions | |
| virtual int | GetFlags () const override |
| Returns a set of bit flags specifying which functions are implemented for this region (see RegFlags). | |
| size_t | AddRegion (Region< N > *reg) |
| adds new region to union | |
| bool | TestPoint (const vector_t &p) const override=0 |
| Returns true if the point is in the region. | |
| int | TestLine (const vector_t &p, const vector_t &dir, vec_type *frac, vector_t *surfp=nullptr, vector_t *surfn=nullptr, vec_type epsilon=0) const override |
| Records the fractions frac1 and frac2 of the line (p,dir) corresponding to the intersections surfpi=p+fraci*dir, surfni - coords of intersection and corresponding outer normal. | |
| virtual RegDumper< N > * | CreateDumper () const override |
| return pointer on object RegDumper, which has function Dump drawing the region | |
| size_t | GetElementarySubRegions (std::vector< int > *flags=nullptr, std::vector< Region< N > * > *oregs=nullptr) const override |
| For composite regions returns the number of elementary subregions, otherwise returns 0. | |
 Public Member Functions inherited from Region< N > | |
| virtual vec_type | SurfProject (const vector_t &p, vector_t *surfp=nullptr, vector_t *surfn=nullptr) const |
| finds the point on the region surface closest to the given one p returns distance to this point (positive is P outside and negative is P inside region), surfp – projection, surfn – norm vector at surfp | |
| template<class contour_t > | |
| vec_type | TestContour (const contour_t &cnt, VecContour< N > *subcont=nullptr, vector_t *subcenter=nullptr) const |
| Returns the area fraction of the contour part that is inside the region, subcontour which is inside the region (if pointer is not nullptr) and the center of the subcontour (if pointer is not nullptr) | |
| virtual vec_type | TestPtrContour (const PtrContour< N > &cnt, VecContour< N > *subcont=nullptr, vector_t *subcenter=nullptr) const |
| virtual version of TestContour for particular PtrContour | |
| virtual vector_t | GetBoundingBox (vector_t *v1, vector_t *v2) const |
| Returns opposite corners of the box which contains the region inside itself. | |
| virtual vector_t | GetCenter () const |
| Returns the center of the region. | |
| virtual vec_type | Volume () const |
| Returns volume of the region. '-1' means that function is not implemented. | |
| virtual vec_type | GetInsideEdgePart (const vector_t &p1, const vector_t &p2) const |
| Returns a fraction of the edge [0-1] that belongs to the region. | |
| virtual vec_type | TestEdge (const vector_t &p1, const vector_t &p2, vector_t *surfp=nullptr, vector_t *surfn=nullptr) const |
| Returns a fraction of the edge from the first point till the intersection with the surface of the region. | |
| virtual vec_type | TestRay (const vector_t &p1, const vector_t &dir, vector_t *surfp=nullptr, vector_t *surfn=nullptr, vec_type epsilon=0) const |
| Returns the fraction of the ray corresponding to the nearest intersection in positive direction frac<0 means no intersection in positive direction intersections with frac<=epsilon are ignored. | |
Additional Inherited Members | |
| Public Types inherited from Region< N > | |
| typedef unknown_cat | category |
| Category of the region to determine the correct template behaviour for various algorithms (see Body categories categories). | |
Detailed Description
template<int N>
class CompositeRegion< N >
class CompositeRegion< N >
union of arbitrary number of regions
Member Function Documentation
◆ GetElementarySubRegions()
template<int N>
|
inlineoverridevirtual |
For composite regions returns the number of elementary subregions, otherwise returns 0.
Optionally fills subregion flags and inters to all subregions found. Should be recursively called for composite regions with arbitrary components.
Reimplemented from Region< N >.
◆ TestLine()
template<int N>
|
inlineoverridevirtual |
Records the fractions frac1 and frac2 of the line (p,dir) corresponding to the intersections surfpi=p+fraci*dir, surfni - coords of intersection and corresponding outer normal.
Intersections with frac<=epsilon are ignored. Returns the number of intersections: 0, 1 (touching or intersection of infinite region) or 2 because region is convex.
Reimplemented from Region< N >.
The documentation for this class was generated from the following file:
